1.Introduction
1.1intro
图的表示学习:大致来说就是将原始的结点(或链接、或图)表示为向量(嵌入embedding),图中相似的结点会被embed得靠近(指同一实体,在结点空间上相似,在向量空间上就也应当相似)。
1.2Applications of Graph ML
node level:
protein folding:给定氨基酸序列计算预测蛋白质的3D结构。模拟蛋白质位置,预测3Dshape。
edge level:
recommender systems :pinsage图像+图结构,更好的推荐 ;任务目标是使相似结点嵌入之间的距离比不相似结点嵌入之间的距离更小。
药物组合副作用:预测引擎,蛋白质相互作用网络,预测缺失的边缘。
背景:很多人需要同时吃多种药来治疗多种病症。任务:输入一对药物,预测其有害副作用。
subgraph level:
Google map: traffic prediction测一段路程的长度、耗时等:将路段建模成图,在每个子图上建立预测模型
graph level:
用GNN的图分类任务来从一系列备选图(分子被表示为图,结点是原子,边是化学键)中预测最有可能是抗生素的分子;
预测材料变形:用GNN来预测粒子的下一步活动(组成一个新位置、新图
1.3design choice:
Bipartite Graph→Folded/Projected Bipartite Graphs
Representing Graphs:Edge list【难表示】;Adjacency list【对图的分析和操作更方便】
结点和边的属性:Weight (e.g., frequency of communication);Ranking (best friend, second best friend…);Type (friend, relative, co-worker);Sign: Friend vs. Foe, Trust vs. Distrust;Properties depending on the structure of the rest of the graph: Number of common friends
Self-edges (self-loops)自环 / Multigraph
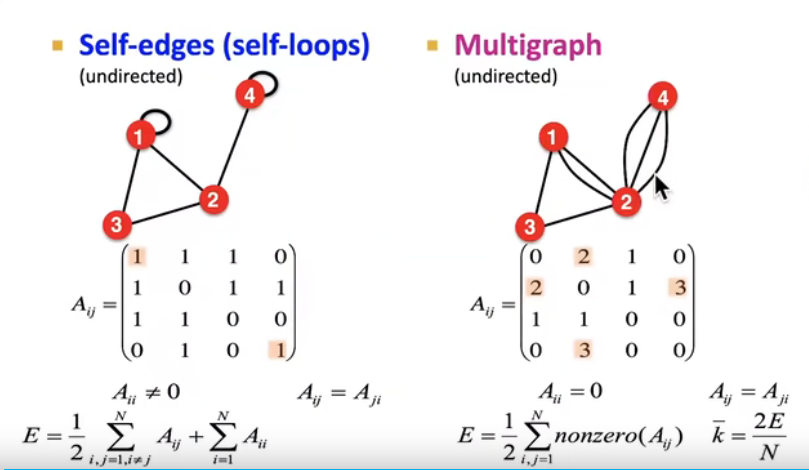
multigraph有时也可被视作是weighted graph,就是说将多边的地方视作一条边的权重(在邻接矩阵上可看出效果是一样的)。但有时也可能就是想要分别处理每一条边,这些边上可能有不同的property和attribute
Connectivity
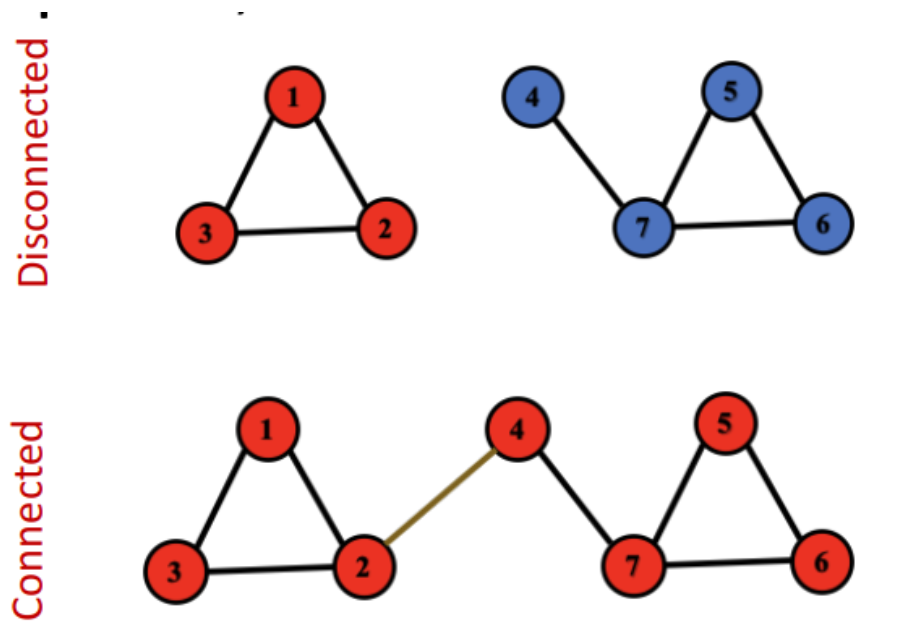
connected:任意两个结点都有路径相通 strongly connected components:互相可以访问
disconnected:由2至多个connected components构成。
最大的子连接图:giant component
isolated node
这种图的邻接矩阵可以写成block-diagonal的形式,数字只在connected components之中出现。【聚类中的块对角个数=类别数】
2.Feature Engineering for ML in Graphs
传统pipelines【2 steps】:设计并获取所有训练数据上结点/边/图的特征→分类器/模型→新结点作出预测
Features: d-dimensional vectors
Objects: Nodes, edges, sets of nodes, entire graphs
Objective function: What task are we aiming to solve?
2.1Node Level Feature
1.Importance-based features考虑了结点的重要性;
2.Structure-based features捕获节点附近的拓扑属性
eigenvector centrality:如果结点邻居重要,那么结点本身也重要。与link的数量无关,与link的重要性有关。

betweenness centrality:桥梁!如果一个结点处在很多结点对的最短路径上,那么这个结点是重要的。
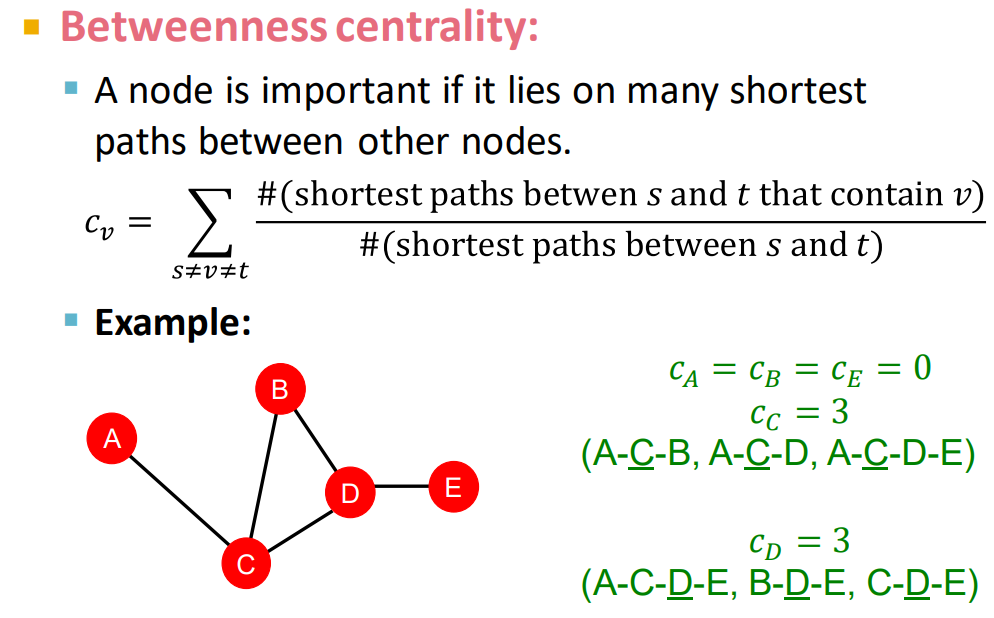
closeness centrality:交通枢纽!到其他结点的路径长度最小。越居中越短。
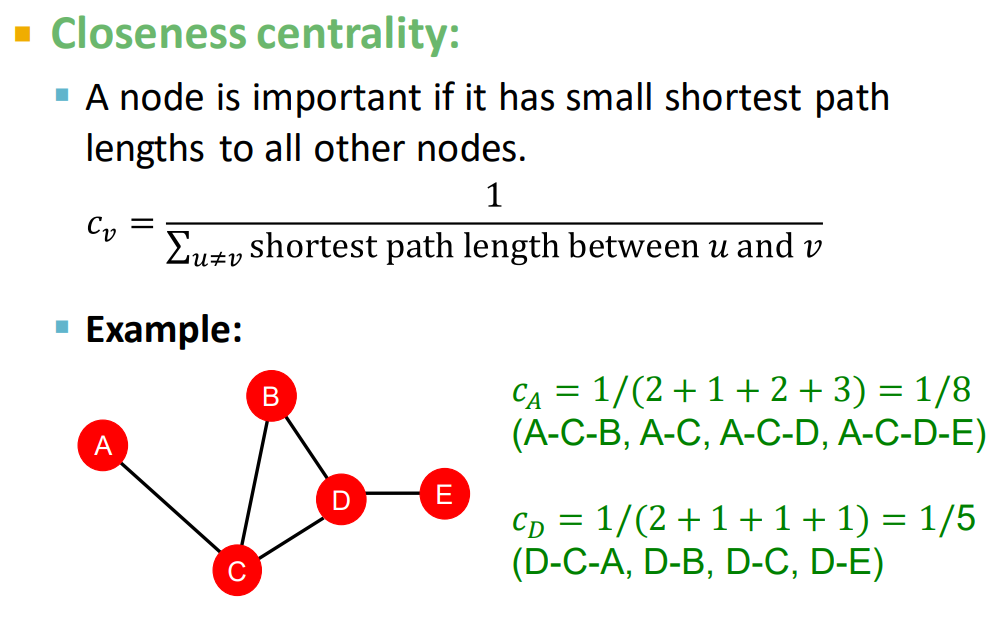
clustering coefficient聚类系数:邻居的联系程度
第1个例子:6 / 6
第2个例子:3 / 6
第3个例子:0 / 6
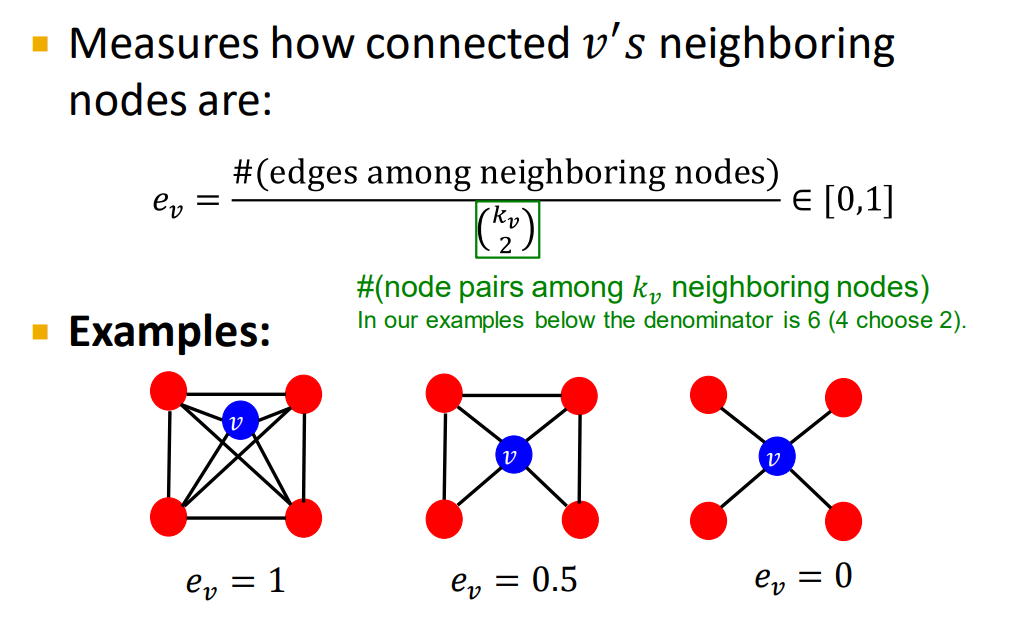
三角形/三元组:结点自我网络。共友也会互相认识。
三角形可以拓展到某些预定义的子图pre-specified subgraph
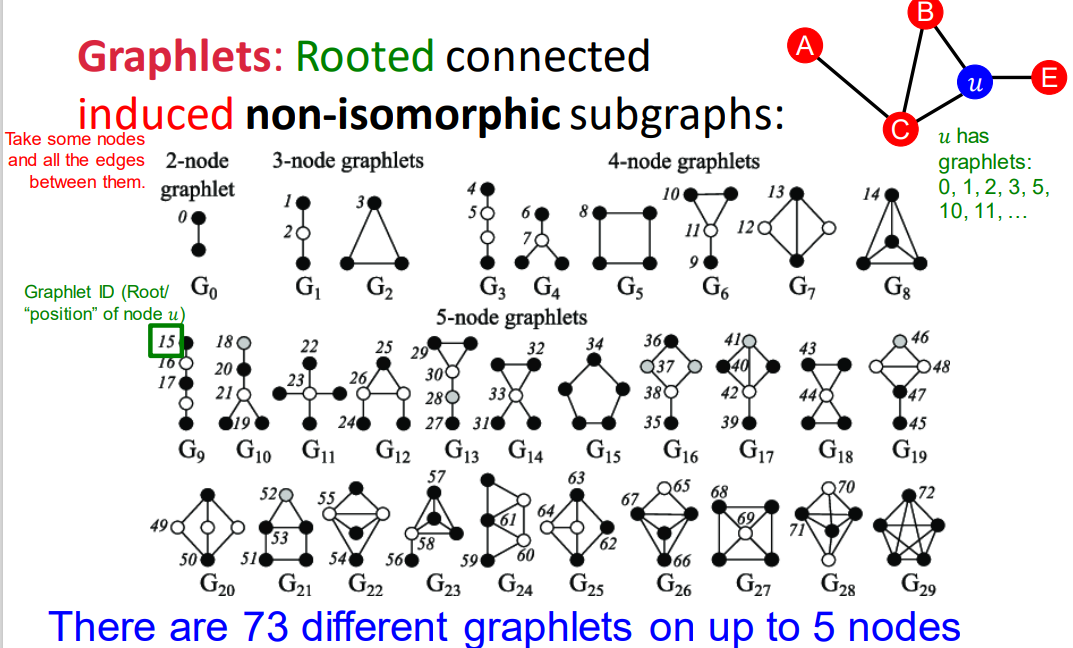
graphlets
2-5个节点的graphlets,可以得到一个长度为73个坐标coordinate的向量GDV,描述该点的局部拓扑结构topology of node’s neighborhood,可以捕获距离为4 hops的互联性interconnectivities。
相比节点度数或clustering coefficient,GDV能够描述两个节点之间更详细的节点局部拓扑结构相似性local topological similarity。
2.2Link Level Feature
link level prediction:根据网络现有的link预测新的link
eg基于相似性:算两点间的相似性得分(如用共同邻居衡量相似性),然后将点对进行排序,得分最高的n组点对就是预测结果,与真实值作比
测试阶段:评估无edge的node pairs→rank k→prediction
链接预测任务的两种类型:
随机缺失边【第一种假设可以以蛋白质之间的交互作用举例,缺失的是研究者还没有发现的交互作用。新链接的发现会受到已发现链接的影响。在网络中有些部分被研究得更彻底,有些部分就几乎没有什么了解,不同部分的发现难度不同】;随时间推演边【以社交网络举例,随着时间流转,人们认识更多朋友。】
distance-based feature
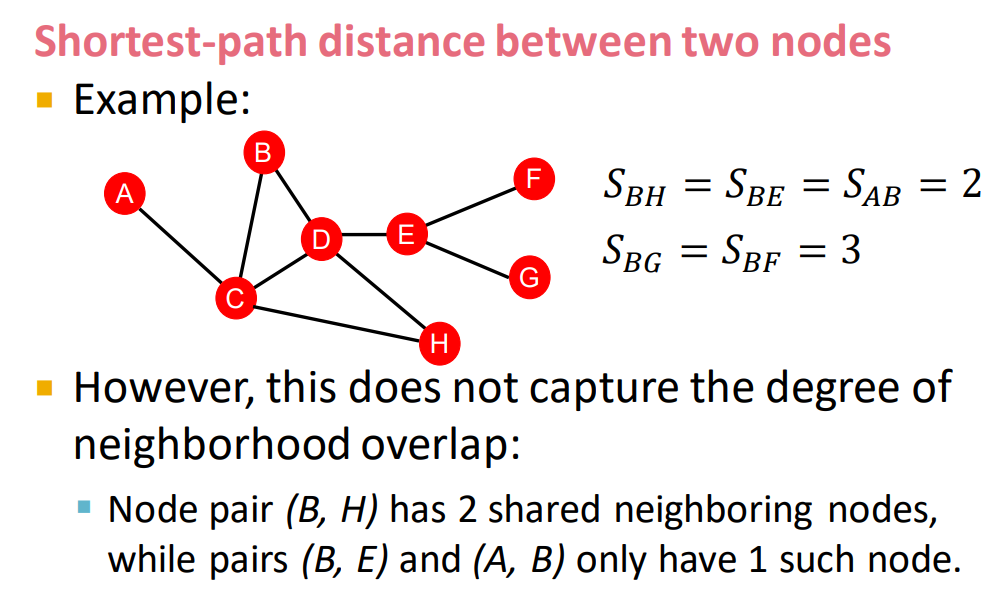
local neighborhood overlap
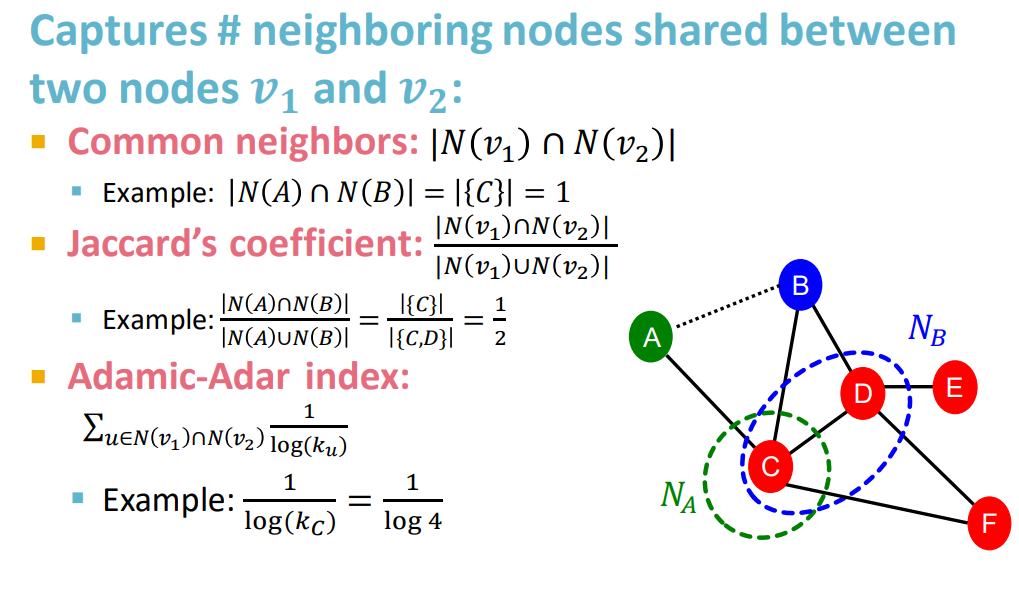
common neighbors: 度数高将表现结果更高。
Adamic-Adar index:有点像信息熵,度数低的共友比名人共友价值大。
如果没有共友的情况,则值为0。【缺点:两个点未来仍有可能被连接起来。相距两跳的结点、没有邻居的结点?解决方案global neighborhood overlap】
global neighborhood overlap
获得一对结点的得分。
Katz index:计算node pairs之间所有长度路径的数量 → 对邻接矩阵求幂
邻接矩阵:代表u和v之间长度为1的路径的数量
分解路径:将长度为1转化,通过桥接方法。对起始节点和相邻结点求和,到目标结点。【归纳法】

观察其对角线,其实就是邻居的数量。

比较长的距离以比较小的权重。
2.3Graph Level Feature
核方法:

eg. BoW for graph:将图表示成一个向量,每个元素代表对应something出现的次数(这个something可以是node, degree, graphlet, color)node degrees

eg. Graphlet kernel【侧重于node 和 edge,即结构 】直接点积两个图的graphlet count vector得到相似性。对于图尺寸相差较大的情况需进行归一化。计算代价高,k-size对应n^k
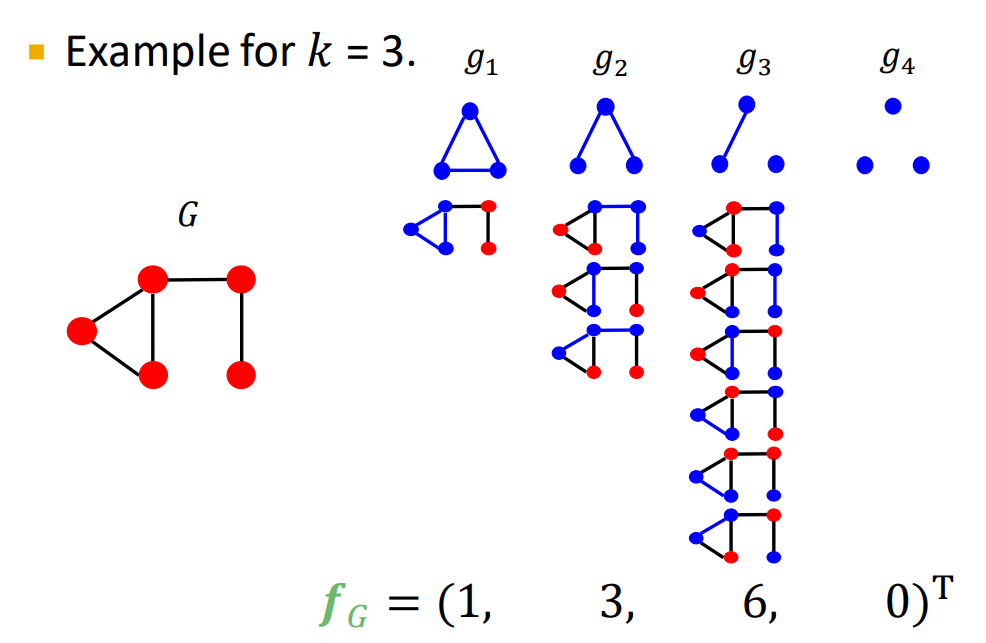
eg. Weisfeiler-Lehman Kernel :建立特征描述子,邻域结构叠代结点度。
color refinement:

把邻居颜色聚集起来,使用hash,重新标记颜色。【优化是线性的】
进行K次迭代,整个迭代过程中颜色出现的次数作为Weisfeiler-Lehman graph feature。上述向量点积计算相似性,得到WL kernel。
3.Node Embeddings
3.1encoder-decoder
graph representation learning:学习到图数据用于机器学习的、与下游任务无关的特征,我们希望这个向量能够抓住数据的结构信息。
将图数据紧密地嵌入到嵌入空间中→自动对结构信息进行编码用于下游任务。
eg. node embedding:deep walk
Encoder and Decoder:对结点进行编码,保证其在嵌入空间的相似性。在二维的相似性【例如距离】,可反应图的结构。
Encoder:将节点映射为embedding
定义一个衡量节点相似度的函数(如衡量在原网络中的节点相似度)
Decoder DEC:将embedding对映射为相似度得分。

ENC(v)=Z · v
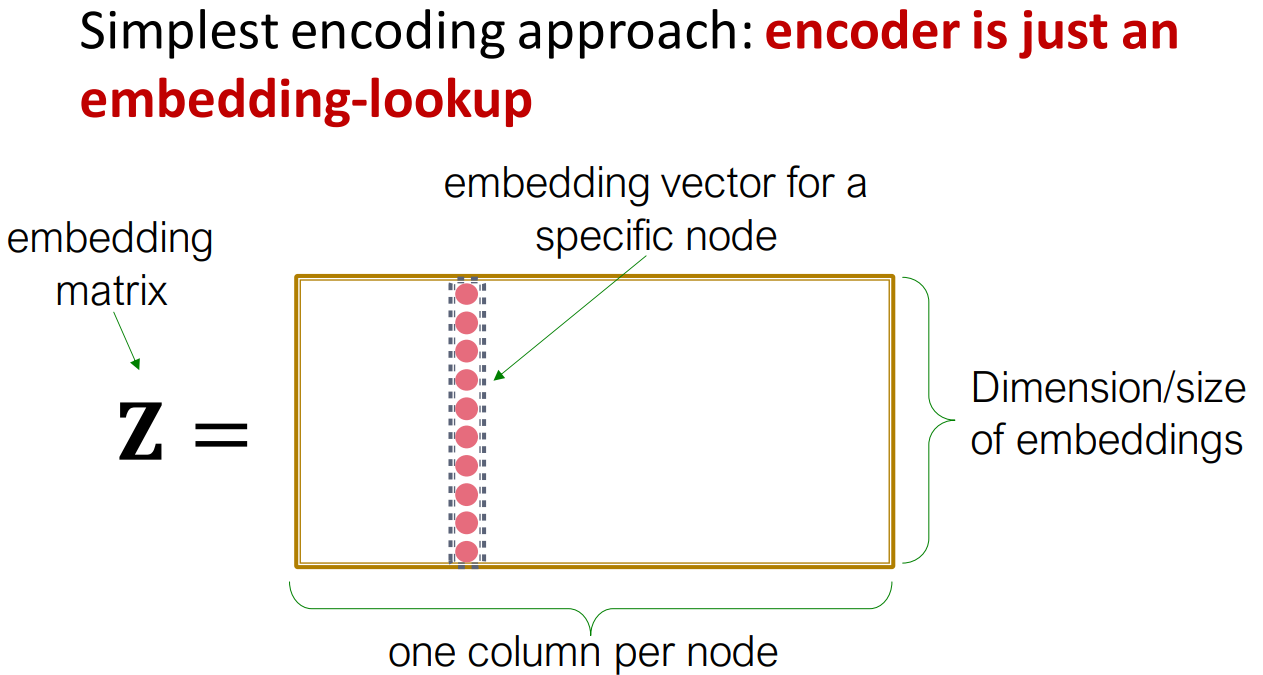
→ Z(d,v)每个节点都有一个列来表示该结点的嵌入。
→v是一个其他元素都为0,对应节点位置的元素为1的向量。
【缺陷:参数过多,难scale up到大型图;Z的大小取决于结点的数量】
DEC:节点相似的不同定义:边;邻居;相似的structural roles
random walks:无监督/自监督→使用结点embedding时,并没有使用结点的label和功能,目标只学习了网络的相似性。
3.2Random Walk Approaches for Node Embeddings
goal:每个结点的嵌入向量z
随机游走的相似性:使用概率表示,从结点u开始随机走动得到v的概率

random walk:从某一结点开始,每一步按照概率选一个邻居,停止后得到随机游走序列。→点u和v在一次随机游走中出现的概率【相似的网络邻居,彼此之间很近,之间可能有多条路径】
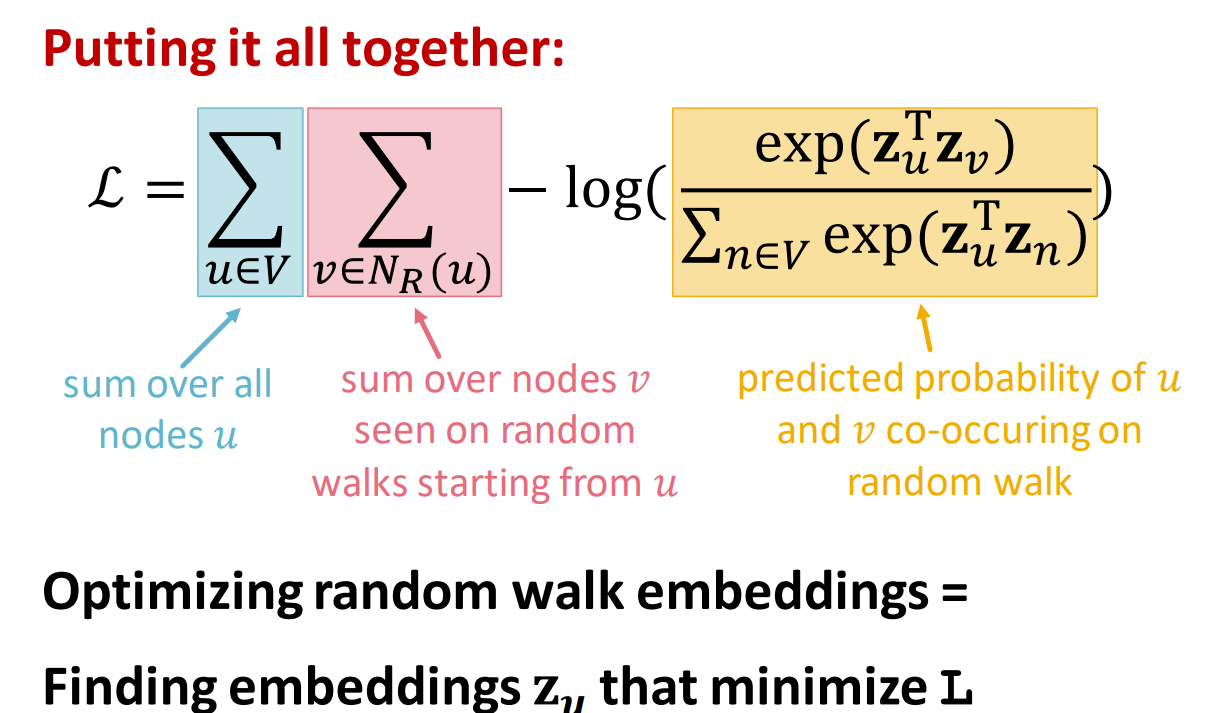
复杂度O(V^2)。改进:softmax归一化的分母。将抽出k个结点作为负样本代替所有结点作为负样本。【k值大相当于加入了更多数据,方差会变小,偏差比较大。】

random walk策略
eg.deep walk:一阶随机游走
eg.node2vec
灵活的网络邻居【local(BFS) and global(DFS)】→丰富的结点嵌入【biased walk】:引入二阶随机数
超参数:p:return parameter【记住游走的来源】;q:DFS和BFS的ratio
例如保持相同的为走到S2,向前迈进为S3/S4。p小则返回,q小则探索。
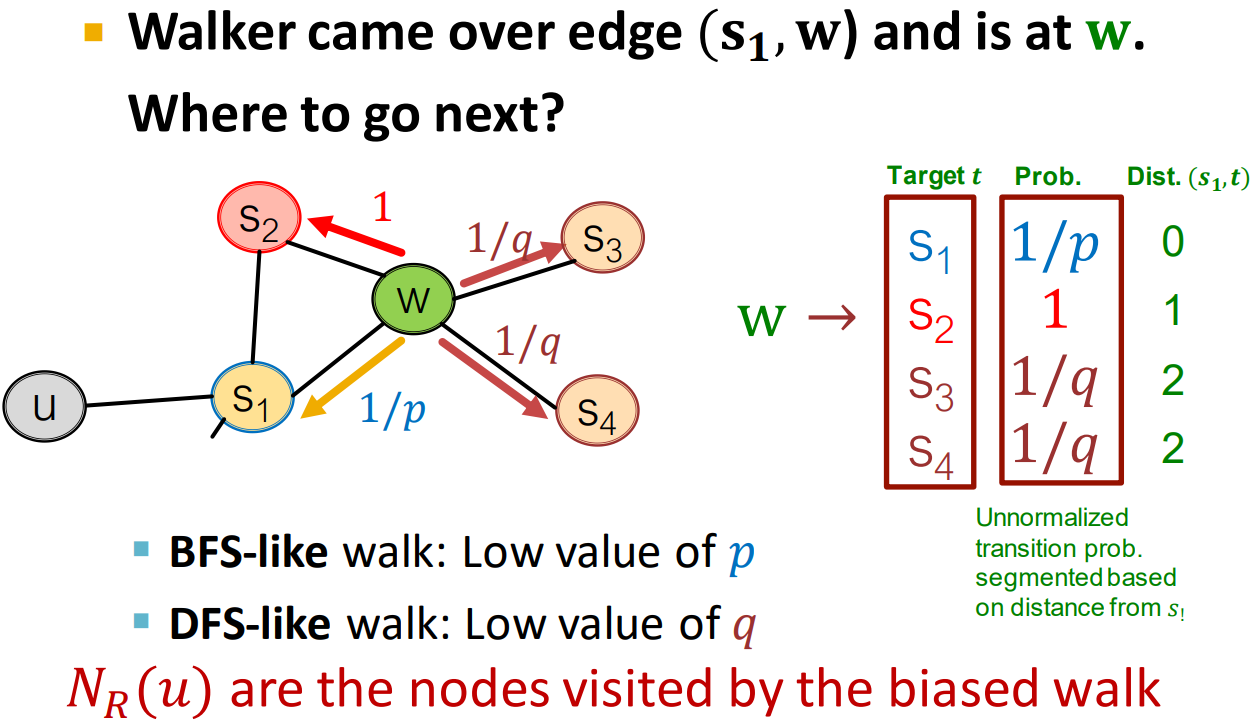
node2vec在节点分类任务上表现更好,不同的方法在不同数据的链接预测任务上表现不同。
3.3 Embedding Entire Graphs
聚合/加权平均结点的嵌入;
introduce a virtual node【虚拟结点将连接到网络中所有其他结点】→嵌入子图/整个图→得到全图的信息;
anonymous walk embeddings:以节点第一次出现的序号(是第几个出现的节点)作为索引。拜访了不同的结点,但用相同的顺序获得相同的anonymous表示。
4.GNN
结点嵌入任务目的:在于将节点映射到d维向量,使得在图中相似的节点在向量域中也相似。使用一个大矩阵直接储存每个节点的表示向量,通过矩阵与向量乘法来实现嵌入过程。缺陷:需要O(V)复杂度的参数,太多结点间参数不共享,每个结点表示的向量都是独特的;无法获取在训练时没出现的结点的表示向量,即transductive;无法应用结点的特征信息。
浅层编码:Encoder+similarity function+Decoder→学习Z矩阵。
深层编码:可以与结点相似性功能结合使用。
4.1 basics of deep learning
supervised learing: x→f→y


梯度向量:函数增长最快的方向和增长率,每个元素是对应参数在损失函数上的偏微分。
方向导数:函数在某个给定方向上的变化率。
梯度是函数增长率最快的方向的方向导数。
迭代:将参数向负梯度方向更新;理想的停止条件是梯度为0,在实践中一般则是用“验证集上的表现不再提升”作为停止条件;学习率是一个需要设置的超参数,控制梯度下降每一步的步长,可以在训练过程中改变。
minibatch SGD:每一次梯度下降都需要计算所有数据集上的梯度,耗时太久→使用SGD的方法,将数据分成多个minibatch,每次用一个minibatch来计算梯度
SGD是梯度的无偏估计,但不保证收敛,所以一般需要调整学习率。
batch size:每个minibatch中的数据点数;iteration:在一个minibatch上做一次训练;epoch:在整个数据集上做一次训练。
前向传播:compute loss starting from input【求下降的多少】
梯度反向传播:计算梯度是不断向后的过程【求偏导,求下降的最快方向】
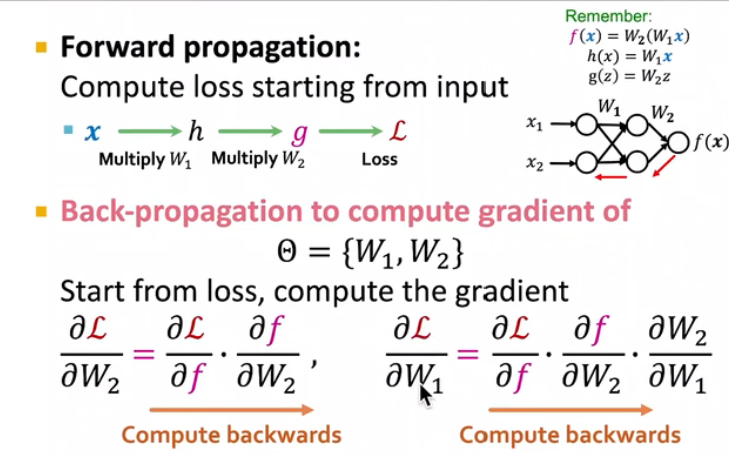
引入非线性:提高表达力
MLP:整合线性和非线性
4.2Deep Learning for Graphs
set up:

naive approach:input【邻接矩阵+node feature 能表示成grid的形式】需要 O(|V|)的参数,不适用于不同大小的图。对节点顺序敏感(我们需要一个即使改变了节点顺序,结果也不会变的模型)
图上无法定义固定的locality或滑动窗口,而且图是permutation invariant【order是不固定的】
Graph Convolutional Networks:通过节点邻居定义其计算图,传播并转换信息,计算出节点表示(可以说是用邻居信息来表示一个节点)
核心思想:通过聚合邻居来生成节点嵌入→通过神经网络聚合信息【每个结点都能定义】
!在每一层中结点都有不同的嵌入【节点在每一层都有不同的表示向量,每一层节点嵌入是邻居上一层节点嵌入再加上它自己(相当于添加了自环)的聚合。】 k 跳对应k layers;聚合顺序无关紧要 a set of elements
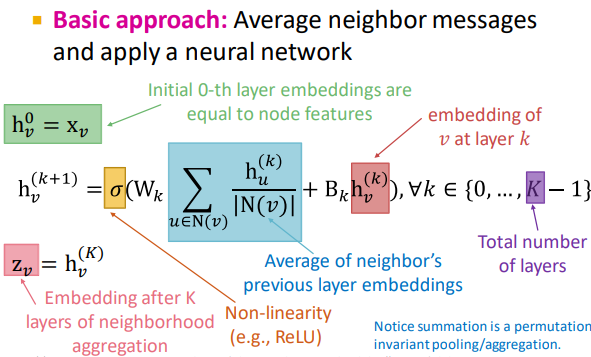
模型上可以学习的参数【只取决于嵌入的大小,而非图形的大小】:W 邻居聚合权重;B 转换结点本身隐藏向量的权重
网络中所有的结点都使用相同的更新公式。
使用matrix表示:H 来自上一层结点的嵌入


训练:
有监督使用标签;无监督使用图结构【即相似度】
定义邻域聚合函数→定义loss函数→set of datasets→为新结点生成嵌入【inductive】
5.General Perspective on GNNS
5.1design space
aggregation
message
GNN layers connectivity即组合layers的方式
manipulation:使原始输入图和应用在GNN中的计算图不完全相同(即对原始输入进行一定处理后,再得到GNN中应用的计算图)
learning
5.2 single GNN layer
message:self message【来自上一层结点的嵌入】+neighborhoods‘→转换消息
aggregation:聚合消息【阶不变】eg:求和、平均、最大值
在这两步上都可以用非线性函数(激活函数)来增加其表现力。
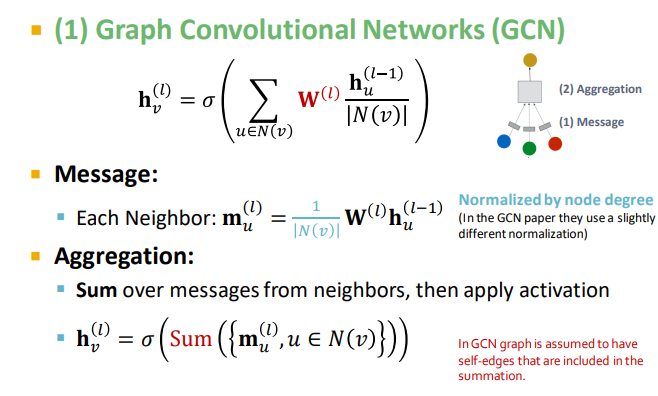

GCN:
message:对上一层的节点嵌入用本层的权重矩阵进行转换,用节点度数进行归一化
agg:sum信息,应用激活函数
GraphSAGE在GCN上的延展:1.聚合函数可以是任意的:AGG 2.从结点本身获得消息和邻居信息3.L2归一化
2 stages→agg:聚合neighborhood信息;将上一层信息与节点本身信息进行聚合
message:在agg过程中一起实现
GAT:【邻居的重要性】
在GCN和GraphSAGE中,直接基于图结构信息(节点度数)显式定义注意力权重,相当于认为节点的所有邻居都同样重要(注意力权重一样大)。
GAT中注意力权重:attention mechanism:alpha→用两个节点上一层的节点嵌入计算其注意力系数
mechanism:alpha的形式:可以使用一个layer 难以收敛【改进:多头注意力 三种功能的注意力再汇总,随机初始化,使用不同的函数,每一个alpha收敛到一个局部最小值】
5.3 stacking GNN layers
over smoothing:如果GNN层数太多,不同节点的嵌入向量会收敛到同一个值。随着K layers增加和hops的增加,nodes感受野增加也很快。图信号越来越弱。
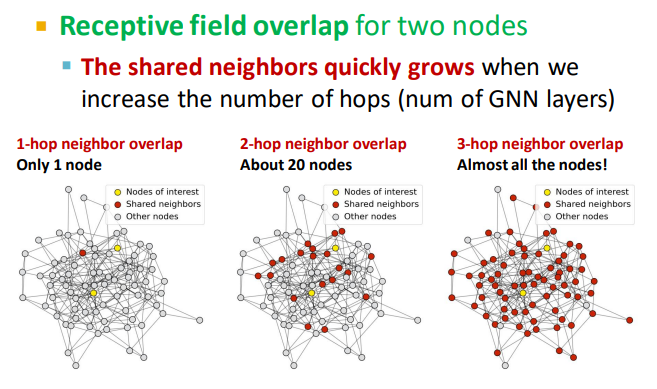
【idea:如何解决GNN的 over smoothing】分析解决问题所需的必要感受野;设置GNN层数 L 略大于我们想要的感受野
增加浅层GNN的表现力:将message和agg过程变成深度神经网络→mlp+pre-layer+post-layer
增加跳层连接:靠前的GNN层可能能更好地区分节点,最终节点嵌入中增加靠前GNN层的影响力,实现方法是在GNN中直接添加捷径,保存上一层节点的嵌入向量。
5.Applications of Graph Neural Networks
由原始图定义的计算图 →针对这一假设改进【输入图并非一定是最佳计算图】
node level:输入图可能缺少功能、属性,或者难以encode;→进行特征增强
graph structure:过于稀疏,消息传递需要多次,效率低。过于密集,消息传递代价高,或者图过大GPU难以使用。
5.1 Graph Augmentation for GNNs
Feature Augmentation:某些结构缺少或者很难学习
例如在化学中判断结点是否处于一个循环中。在计算图中看起来是一样的。3和4个结点的循环,因为度数相同(都是2),所以无论环上有多少个节点,GNN都会得到相同的计算图(二叉树),无法分别。解决方法是为循环增加one-hot编码。
constant node feature& one-hot feature
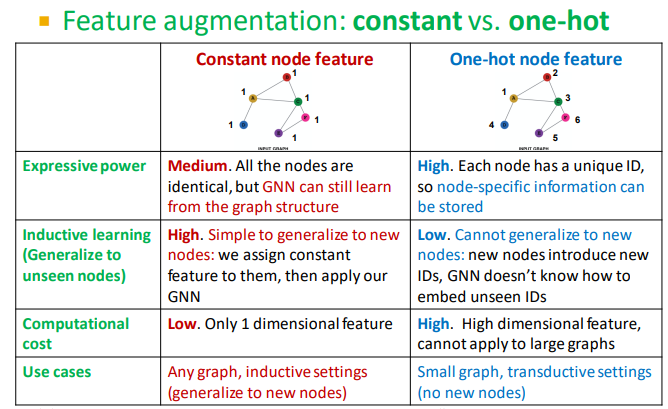
其他常用于数据增强的特征:clustering coefficient,centrality,page rank
Structure Augmentation
稀疏图:
增加虚拟边,邻接矩阵的幂次相加【相当于和朋友的朋友成为了朋友,两跳也相连】
增加虚拟结点,两结点相距过远,牵线搭桥,使得网络不用太大
稠密图:
random sample 折衷,计算效率增加但是会使得信息存在丢失
5.2 training
不同粒度下的prediction head:节点级别,边级别,图级别
node-level:使用node embedding做预测 →k classification/regression 将d维嵌入映射到k维输出
edge-level:使用两个node embedding做预测:可以是像注意力机制那样一个点对另一个点剪→alpha对应边,再使用linear将2d维映射到k维输出;也可以是1 way→点积 k way→多头注意力
graph-level:每个node聚合 pooling。小图上表现很好→mean方法:结果不受节点数量的影响;sum方法:关心图的大小等信息。在大图上的global pooling方法可能会面临丢失信息的问题,效果不好。解决方案:分层聚合,子集比较。【idea:diffPool 分层、差分池】
【缺陷:global pooling采用大量信息】
prediction&labels
有监督学习supervise learning:直接给出标签(如一个分子图是药的概率)node-level:引文论文属于的学科 edge-level:交易中是否有欺诈行为 graph-level:药物的毒性
无监督学习unsupervised learning / self-supervised learning:使用图自身的信号(如链接预测:预测两节点间是否有边)无需外部标签【node-level:节点统计量(如clustering coefficient3, PageRank4 等)edge-level:链接预测(隐藏两节点间的边,预测此处是否存在链接)graph-level:图统计量(如预测两个图是否同构)】
loss
分类 CE

回归 MSE

data split【idea:关于图结构的data split】
训练集是可以用来调整GNN参数的。验证集可以用来调整训练的策略,超参。
fixed split:只切分一次数据集,此后一直使用这种切分方式
random split:随机切分数据集,应用多次随机切分后计算结果的平均值
图结构的特殊性,如果直接像普通数据一样切分图数据集,不能保证测试集隔绝于训练集。【测试集里面的数据可能与训练集里面的数据有边相连,在message passing的过程中就会互相影响,导致信息泄露。】
解决方案:tranductive setting:输入全图在所有split中可见【测试集、验证集、训练集在同一个图上,整个数据集由一张图构成】→仅切分(节点)标签【仅适用于节点/边预测任务】。inductive setting:去掉各split之间的链接,得到多个互相无关的图。【测试集、验证集、训练集分别在不同图上,整个数据集由多个图构成】这样不同split之间的节点就不会互相影响。→因此可以泛化【适用于节点/边/图预测任务】
